वर्गमूल निकालने का सूत्र -वर्गमूल निकालने का तरीका

इस पोस्ट में, हमने  वर्गमूल निकालने का सूत्र -वर्गमूल निकालने का तरीका से संबंधित सभी महत्वपूर्ण बातों को शामिल किया है। जैसे वर्गमूल निकालने का सूत्र वर्गमूल कैसे निकाले ? 

मुख्य गुणन विधि द्वारा वर्गमूल, विभाजन विधि द्वारा वर्गमूल कैसे ज्ञात करें इन टॉपिक की सभी महत्वपूर्ण जानकारी दी गयी है।

वर्गमूल निकालने का सूत्र  

The square root of any number is equal to a number that, when squared, gives the original number.

मान लीजिए कि m एक धनात्मक पूर्णांक है, जैसे कि

\sqrt{m\times m} = \sqrt{m^2} = m 

नोट: एक ऋणात्मक संख्या का वर्गमूल एक जटिल संख्या का प्रतिनिधित्व करता है।

👉 </span>\sqrt{-n} = i\sqrt{n} जहां i काल्पनिक संख्या है।

वर्गमूल के कुछ गुण

• यदि एक संख्या एक पूर्ण वर्ग संख्या है, तो एक पूर्ण वर्गमूल मौजूद है।

• यदि संख्या शून्य संख्या (0 के) के साथ समाप्त होती है, तो इसका एक वर्गमूल हो सकता है।

• दो वर्गमूल मानों को गुणा किया जा सकता है। उदाहरण के लिए,√3 को√2 से गुणा किया जा सकता है, फिर परिणाम √6 होना चाहिए।

• जब दो समान वर्गमूल गुणा किए जाते हैं, तो परिणाम एक मूल  संख्या होना चाहिए। इसका अर्थ है कि परिणाम एक गैर-वर्ग मूल संख्या है। उदाहरण के लिए, जब√7 को √7 से गुणा किया जाता है, तो प्राप्त परिणाम 7 होता है।

• किसी भी नकारात्मक संख्या का वर्गमूल परिभाषित नहीं है। क्योंकि पूर्ण वर्ग ऋणात्मक नहीं हो सकता है।

• यदि कोई संख्या 2, 3, 7 या 8 (इकाई अंक में) के साथ समाप्त होती है, तो सही वर्गमूल मौजूद नहीं है।

• यदि इकाई अंक में 1, 4, 5, 6 या 9 के साथ कोई संख्या समाप्त होती है, तो संख्या में एक वर्गमूल होगा।

वर्गमूल निकालने का  सूत्र 

वर्गमूल निकालने का सूत्र  है:

y = √a

चूंकि, `y.y = y<sup>2</sup> = a`; जहाँ ‘a’ संख्या ‘y’ का वर्ग है।

वर्गमूल कैसे निकाले ?

वर्गमूल को  निकालने के लिए, हम दो विधियों का उपयोग कर सकते हैं: गुणन विधि और  विभाजन विधि।

मुख्य गुणन विधि द्वारा वर्गमूल

एक सही वर्ग संख्या का वर्गमूल मुख्य गुणन विधि का उपयोग करके गणना करना आसान है। आइए हम यहां कुछ उदाहरणों को हल करते हैं

16    2x2x2x2 √16 = 2×2 = 4

144    2x2x2x2x3x3 √144 = 2x2x3 = 12

256     2×2×2×2×2×2×2×2 √256 = (2x2x2x2) = 16

भाग विधि / विभाजन विधि द्वारा वर्गमूल कैसे ज्ञात करें

अपूर्ण संख्याओं के लिए वर्गमूल निकालना थोड़ा मुश्किल है लेकिन हम एक लंबी विभाजन विधि का उपयोग करके गणना कर सकते हैं। इसे नीचे दिए गए उदाहरण की मदद से समझा जा सकता है। 

Step-1: सर्वप्रथम दी गई संख्या के अंको का इकाई से शुरू करके दो-दो अंकों जोड़ा बनाते हैं. यदि कोई अंक अकेला बचता है तो उसे भी एक जोड़ा मान लिया जाता हैं

Step-2: बांयी तरफ से सबसे पहले जोड़े या अंक में ऐसी संख्या का भाग देते है जिसका वर्ग उस जोड़े  के बराबर अथवा उससे कम हो, इस संख्या को भाजक और भागफल के स्थान पर लिखा जाता हैं |  शेषफल ज्ञात करने के लिए पहले जोड़े में से भाजक के वर्ग को उस संख्या में से  घटाते हैं |

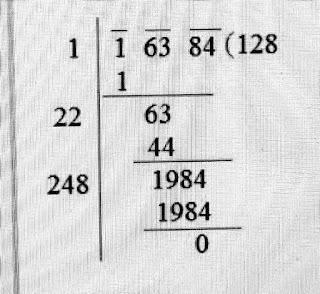
 Q .√16384 का वर्ग मूल भाग विधि द्वारा निकाले