बायो-सेवर्ट नियम विद्युत चुंबकत्व के तहत एक समीकरण है जो एक बिंदु पर प्रवाहित धारा द्वारा उत्पादित चुंबकीय क्षेत्र B का मान बताता है।
सदिश राशि B , परिमाण, दिशा, लंबाई और बिंदु से दूरी पर निर्भर करती है। यह नियम केवल स्थिर अवस्था में ही मान्य है और इससे प्राप्त B के मान एम्पीयर के नियम और गॉस के नियम से प्राप्त चुंबकीय क्षेत्र के अनुरूप हैं।
बायो-सेवर्ट नियम क्या है ?
इस नियम अनुसार धारावाही चालक के कारण किसी बिंदु पर चुंबकीय क्षेत्र ज्ञात किया जाता है एक समीकरण है जो एक बिंदु पर प्रवाहित धारा द्वारा उत्पादित चुंबकीय क्षेत्र B का मान बताता है।
बायो सेवर्ट का नियम का व्यंजक सत्यापन
बायो – सेवर्ट के नियम द्वारा किसी धारावाही चालक के कारण किसी बिन्दु पर चुम्बकीय क्षेत्र ज्ञात किया जाता है । धारा अवयव ( Current Element ) धारावाही चालक तार के किसी अल्पांश की लम्बाई dl और उसमें से बहने वाली धारा I के गुणनफल को धारा अवयव कहते हैं ।
धारा अवयव एक सदिश राशि है । इसकी दिशा धारा प्रवाह की दिशा में होती है ।
किसी धारावाही चालक के एक अल्पांश dl के द्वारा किसी बिन्दु P पर उत्पन्न चुम्बकीय क्षेत्र B का मान
बिंदु P पर चुंबकीय क्षेत्र की तीव्रता
dB ∝ I ( धारा )
dB ∝ dl (अल्पांश की लंबाई )
अल्पांश की लंबाई द्वारा बिंदु p को मिलाने वाली रेखा के बीच बने कोण dB ∝ sinθ
अल्पांश से बिंदु p तक की दूरी dB ∝ 1/r2
बायो सेवर्ट नियम का सूत्र
बायो- सावर्ट का नियम वेक्टर रूप
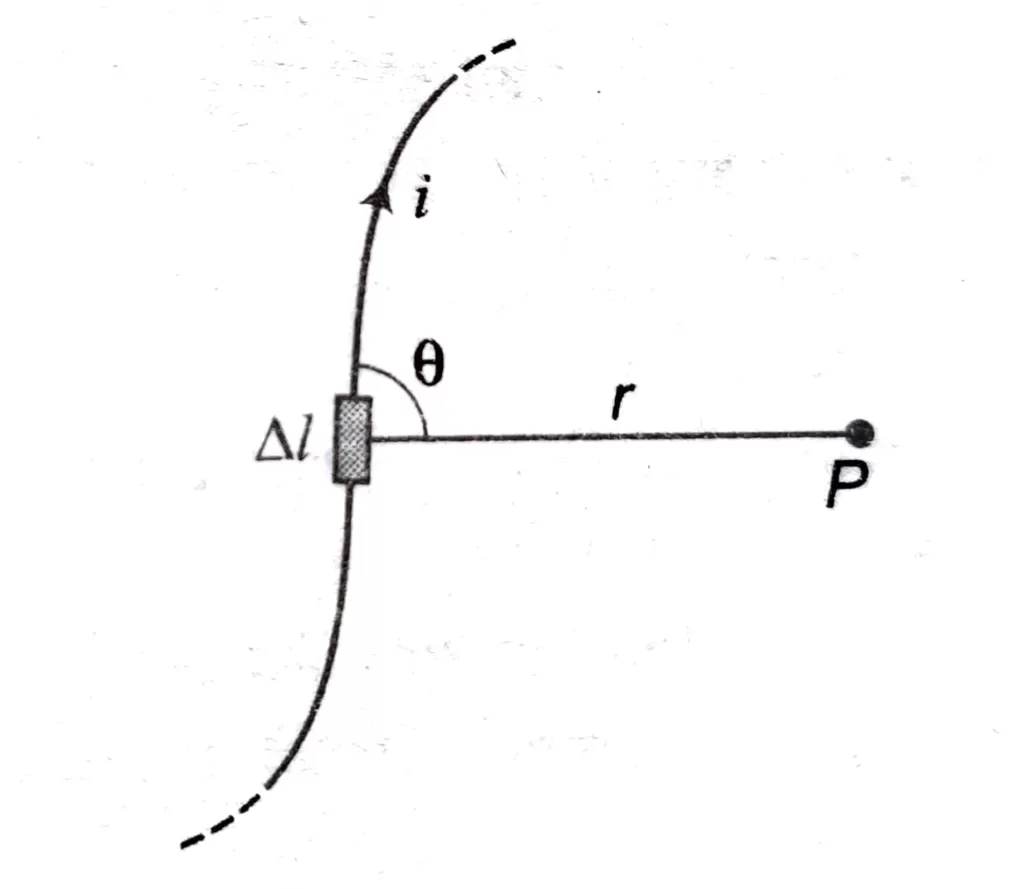
चालक में प्रवाहित धारा के अनुक्रमानुपाती होता है।
चालक के उस अल्पांश की लम्बाई Δl के अनुक्रमानुपाती होता है।
अल्यांश की लम्बाई और अल्पांश को बिन्दु P से मिलाने वाली रेखा के बीच बने कोण की ज्या के समानुपाती होता है।
यह बिन्दु P की अल्पांश से दूरी r के वर्ग के व्युक्कमानुपाती होता है
जहाँ समानुपाती नियतांक है। इसका मान 10-7 वेबर/ऐम्पियर-मी है।
μ0 निर्वात की चुम्बकशीलता है।
μ0 का विमीय सूत्र होता है।
बायो-सेवर्ट के नियम का वेक्टर स्वरूप
dB की दिशा की दिशा में होती है।धारा घनत्व के पदों में बायो-सेवर्ट का नियम
यदि dl व r परस्पर समान्तर हों अर्थात् तो B=0
जब dl व r परस्पर लम्बवत् हों अर्थात्
आवेश तथा आवेश के वेग के पदों में बायो-सेवर्ट का नियम
चुम्बकीय क्षेत्र का मात्रक वेबर/मीटर2 या टेस्ला होता है।
यह नियम वर्ष 1720 में तैयार किया गया था। यह नियम कूलम्ब के नियम के समान है, जिसका उपयोग स्थिर इलेक्ट्रिक्स में किया जाता है।
बायो – सावर्ट नियम के कुछ तथ्य
- यह नियम केवल सममित आवेश वितरणों के लिए लागू होता है ।
- इस नियम को प्रयोग द्वारा सत्यापित नहीं किया जा सकता है ।
- यह नियम केवल छोटी लम्बाई के धारावाही चालकों के लिए लागू होता है ।
- यह नियम स्थिर – वैद्युतिकी ( electrostatics ) में कूलॉम के नियम के समतुल्य होता है ।
- यदि θ=0 या बिन्दु P रेखीय धारावाही चालक की अक्ष पर हो तो dB =0 अर्थात् रेखीय धारावाही चालक के किसी भी बिन्दु पर चुम्बकीय क्षेत्र शून्य होता है ।
बायो-सेवर्ट नियम के अनुप्रयोग
बायो-सेवर्ट नियम के अनुप्रयोग Applications of the Bio-Savart Rule
किसी धारावाही अल्पांश के कारण उत्पन्न चुम्बकीय क्षेत्न
जहाँ μ0, निर्वात की चुम्बकरीलता है।
किसी अनन्त लम्बाई के धारावाही चालक के कारण d दूरी पर उत्पन्न चुम्बकीय क्षेत्र
किसी घारावाछी कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र
किसी परिनालिका के केन्द्र पर चुम्बकीय क्षेत्र
जहाँ N परिनालिका की प्रति एकांक लम्बाई में फेरों की संख्या है
परिनालिका के सिरे पर चुम्बकीय क्षेत्र
| Read more – एनसीईआरटी भौतिक विज्ञान नोट्स |
| Read more – चुम्बक ( Magnet ) | चुम्बकीय क्षेत्र |
| Read more – विद्युत धारा का चुंबकीय प्रभाव |
| Read more – ऐम्पियर के परिपथीय नियम |
