All Math’s formulas for class 10 in Hindi | सभी महत्वपूर्ण गणित के सूत्र कक्षा 10

स्वागत है, इस पोस्ट में All Math’s formulas for class 10 in Hindi | सभी महत्वपूर्ण गणित के सूत्र कक्षा 10 से संबंधित सभी महत्वपूर्ण जानकारी दी गई है। 
maths All formulas 10th class Hindi Main परीक्षा के दौरान सभी छात्रों के पास समय कम होता है। इसलिए उनको एक पेज में सभी फॉर्मूलों की जरूरत होती है और Class 10th maths all Chapter formulas in Hindi इस कमी को देखते हुए हमने ये पोस्ट तैयार की है जिससे आप अच्छे मार्क्स ला सके। 
इस आर्टिकल में all formulas of math’s class 10 ncert in Hindi को समावेश किया है साथ में सभी chapter  के important  mathematics formula class 10 in hindi को अच्छे से लिखा गया है।

  हम उम्मीद करते ये आर्टिकल आपके लिए बहुत उपयोगी होगा। हमारा आपसे बस एक निवेदन है इस maths formulas 10th class in hindi को आपके सभी दोस्तों के साथ शेयर करना न भूले –
सभी महत्वपूर्ण गणित के सूत्र कक्षा 10 Chapter wise formulas 

Chapter 1 वास्तविक संख्याये (Real number) formulas

👉प्राकृतिक संख्या ⇒ 1,2,3,4, 5, ……..

👉सम संख्या ⇒  2, 4, 6, 8, 10, …… 

👉विषम संख्या ⇒ 1, 3, 5, 7, 9,….. 

👉पूर्णांक संख्या ⇒…, -3,-2,-1, 0,1, 2, 3, ..

👉पूर्ण संख्या ⇒ 0, 1, 2, 3, 4, …… 

👉भाज्य संख्या ⇒ 4, 6, 8, 9, …… 

👉अभाज्य संख्या ⇒ 2, 3, 5,7,11, .. 

👉सह अभाज्य संख्या ⇒ ex. (5, 7), (2, 3) 

👉परिमेय संख्या ⇒ ex. √4 ,7/5, 2/3,3 

👉अपरिमेय संख्या ⇒ ex. √5, √7 ,√11 ,√13 

👉वास्तविक संख्या ⇒ ex. √4 ,√11,4/7,1,6 , 

👉अवास्तविक संख्या ⇒ ex. √-6, √-5, √-29

Chapter 2 बहुपद (Polynomial) formulas

(a+b)^{2}=a^{2}+b^{2}+2 a b

(a-b)^{2}=a^{2}+b^{2}-2 a b

(a+b)(a-b)=a^{2}-b^{2}

(x+a)(x+b)=x^{2}+(a+b) x+a b

(x+a)(x-b)=x^{2}+(a-b) x-a b

(x-a)(x+b)=x^{2}+(b-a) x-a b

(x-a)(x-b)=x^{2}-(a+b) x+a b

(a+b)^{3}=a^{3}+b^{3}+3ab(a+b)

(a-b)^{3}=a^{3}-b^{3}-3ab(a-b)

(x+y+z)^{2}=x^{2}+y^{2}+z^{2} +2 x y+2 y z+2 xz

(x+y-z)^{2}=x^{2}+y^{2}+z^{2}+2 x y-2 y z-2 x z 

(x-y+z)^{2}=x^{2}+y^{2}+z^{2}-2 x y-2 y z +2 x z

(x-y-z)^{2}=x^{2}+y^{2}+z^{2}-2 x y+2 y z-2 x z

x^{3}+y^{3}+z^{3}-3xyz=(x+y+z)(x^{2}+y^{2}+z^{2}-x y-y z-x z)

x^{2}+y^{2}=1 / 2[(x+y)^{2}+(x-y)^{2}]

(x+a)(x+b)(x+c)=x^{3}+(a+b+c) x^{2}+(a b+b c+c a) x+a b c

x^{3}+y^{3}=(x+y)(x^{2}-x y+y^{2})

x^{3}-y^{3}=(x-y)(x^{2}+x y+y^{2})

x^{2}+y^{2}+z^{2}-x y-y z-z x=1/2[(x-y)^{2}+(y-z)^{2}+(z-x)^{2}]

👉यदि द्विघात बहुपद ax²+bx+c के मूल / शून्यक \alpha,\beta हों, तो

\alpha+\beta=-\frac{b}{a}, \quad \alpha \beta=\frac{c}{a}

👉यदि \alpha, \beta, \gamma त्रिघात बहुपद ax³+bx²+cx+d के मूल /शून्यक हों, तो

\alpha+\beta+\gamma=\frac{-b}{a}, \quad
\alpha \beta+\beta \gamma+\gamma \alpha=\frac{c}{a}, \quad
\alpha \beta \gamma=\frac{-d}{a}

Chapter-3 दो चरो वाले रैखिक समीकरण युग्म
(Pair of linear equations in two variables)  formulas

👉एक रैखिक समीकरण युग्म को निम्न दो तरीको से हल किया जा सकता है

(i) ग्राफीय विधि द्वारा

(ii) बीजगणितीय विधि द्वारा

👉ग्राफीय विधि द्वारा एक रैखिक समीकरण युग्म को हल करना

दो चर में एक रेखीय समीकरण युग्म का ग्राफ दो रेखाओ द्वारा दर्शाया जाता है।

(i) यदि रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं तो, वह बिंदु दोनों समीकरण का अद्वितीय हल होता है। इस स्थिति में, समीकरण युग्म संगत होता है।

(ii) यदि रेखाएँ संपाती हैं, तो उसके अपरिमित रूप से अनेक हल होते हैं-रेखा पर स्थित प्रत्येक बिंदु हल होता है। इस स्थिति में, समीकरण युग्म आश्रित ( संगत) होता है।

(iii) यदि रेखाएँ समांतर हैं, तो समीकरण युग्म का कोई हल नहीं होता है। इस स्थिति में, समीकरण युग्म असंगत होता है।

👉बीजगणितीय विधि द्वारा एक रैखिक समीकरण युग्म को हल करना

(i) प्रतिस्थापन विधि

(ii) विलोपन विधि

(iii) वज्न-गुणन विधि

👉यदि दिए गए रैखिक समीकरण a₁x+b₁y+c₁=0 और a₂x+b₂y+c₂=0 एक रैखिक समीकरण युग्म को प्रदर्शित करते हैं,तो

(i) \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} इस स्थिति में, रैखिक समीकरण युग्म संगत होता है।

(ii)

\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}

इस स्थिति में, रैखिक समीकरण युग्म असंगत होता है।

(iii)

\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}

इस स्थिति में, रैखिक समीकरण युग्म आश्रित ( संगत) होता है।

chapter – 4 द्विघात समीकरण ( quadratic equation )  formulas

👉द्विघात समीकरण ax²+bx+c के मूल

\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}

यदि

b^{2}-4 a c \geq 0

हो।

👉द्विघात समीकरण

 a x^{2}+b x+c=0, a \ne 0

में,

(i) दो भिन्न वास्तविक मूल होते हैं, यदि b^{2}-4ac>0

(ii) दो बराबर मूल (अर्थात् संपाती वास्तविक मूल) होते हैं, यदि b^{2}-4 a c=0

(iii) कोई वास्तविक मूल नहीं होते हैं, यदि b^{2}-4 a c<0

Chapter – 5 समान्तर श्रेणी
(Arithmetic progression) formulas

👉A.P. का व्यापक रूप a, a+d, a+2 d, a+3 d, \ldots है।

👉संख्याओं की एक दी हुई सूची A.P. होती है, यदि अंतरों a_{2}-a_{1}, a_{3}-a_{2}, a_{4}-a_{3}, \ldots, से एक ही ( समान ) मान प्राप्त हो, अर्थात् k के विभिन्न मानों के लिए a_{k+1}-a_{k} एक ही हो।

👉प्रथम पद a और सार्व अंतर d वाली A.P. का n वाँ पद (या व्यापक पद) a_n 

👉किसी A.P के प्रथम n पदों का योग S 

सूत्र

S =\frac{n}{2}[2 a+(n-1) d] से प्राप्त होता है।

👉यदि एक परिमित A.P. का अंतिम पद L है, तो इस A.P. के सभी पदों का योग S

सूत्र

Chapter – 6 त्रिभुज (Triangles)

Q.पाइथागोरस प्रमेय सिद्ध करो

Ans –  पाइथागोरस प्रमेय

Chapter – 7 निर्देशांक ज्यामिति
(coordinate geometry)

👉P(x_{1}, y_{1})और Q(x_{2}, y_{2}) के बीच की दूरी –

👉बिंदु P(x, y) की मूलबिदु से दूरी –

👉उस बिंदु P(x, y) के निर्देशांक जो बिंदुओं A(x_{1}, y_{1}) और B(x_{2}, y_{2}) को जोड़ने वाले रेखाखंड को m_{1}: m_{2} के अनुपात में आंतरिक रूप से विभाजित करता है –

(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}})

👉बिंदुआं P(x_{1}, y_{1}) और Q (x_{2}, y_{2}) को जोड़ने वाले रेखाखंड  PQ के मध्यबिदु के निर्देशांक –

(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2})

👉बिंदुआं (x_{1}, y_{1}),(x_{2}, y_{2}) और (x_{3}, y_{3}) से बनने वाले त्रिभुज का क्षेत्रफल 

\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]

Chapter – 8 त्रिकोणमिति परिचय
(introduction trigonometry) formulas

👉समकोण त्रिभुज ABC में, जिसका कोण B समकोण है,

\sin {A}=\frac { AB } { AC }

\cos {A}=\frac{ BC } { AC }

\tan{A}=\frac{ AB} { BC }

\cosec A=\frac{1}{\sin A}

\sec A=\frac{1}{\cos A} 

\tan A=\frac{1}{\cot A}

\tan A=\frac{\sin A}{\cos A}

\sin (90^{\circ}-A)=\cos A

\cos (90^{\circ}-A)=\sin A

\tan (90^{\circ}-A)=\cot A

\cot (90^{\circ}-A)=\tan A

\sec (90^{\circ}-A)=\cosec A

\cosec(90^{\circ}-A)= \sec A

\sin ^{2} A+\cos ^{2} A=1

\sec ^{2} A-\tan ^{2} A=1 \quad  0° ≤ θ < 90°

\cosec^{2}A=1+\cot ^{2}A \quad 0° ≤ θ ≤ 90°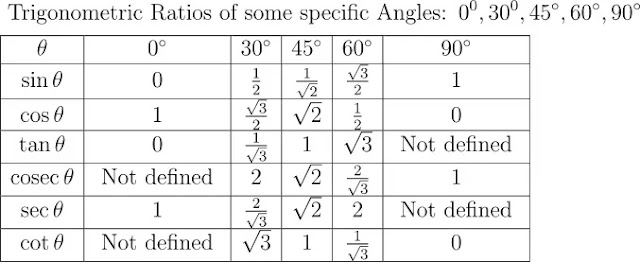

Chapter – 9 त्रिकोणमिति के कुछ अनुप्रयोग
(Some applications of trigonometry)formulas

(ii) यदि हमे किसी वस्तु को देखने के लिए अपने सिर को ऊपर की तरफ उठाये  अथार्थ जब क्षैतिज रेखा से बना कोण क्षैतिज से ऊपर हो तो वह कोण  उन्नयन कोण होता  है 

(iii) यदि हमे किसी वस्तु को देखने के लिए अपने सिर को नीचे की तरफ झुकाना पड़े  अथार्थ जब क्षैतिज रेखा से बना कोण क्षैतिज से नीचे हो तो वह कोण अवनमन कोण होता  है 

Chapter – 10 वृत्त (Circle) | Chapter – 12 वृत्त से संबंधित क्षेत्र (Area related to circle) formulas

👉वृत्त की परिधि = 2\pi r

👉वृत्त का क्षेत्र = \pi r^2

👉θ कोण के क्षेत्र का क्षेत्रफल = (θ/360) × \pi r^2

👉θ कोण के एक क्षेत्र की चाप की लंबाई  = (θ/360) × 2 \pi r

(r = वृत्त की त्रिज्या )

Chapter – 13 पृष्ठीय क्षेत्रफल एवं आयतन
(Surface areas and Volume) formulas

घनाभ का पृष्ठीय क्षेत्रफल =2({lb}+{bh}+{hl})

घन का पृष्ठीय क्षेत्रफल =6 a^{2}

बेलन का वक्र पृष्ठीय क्षेत्रफल =2 \pi r h

बेलन का कुल पृष्ठीय क्षेत्रफल =2 \pi r(r+h)

शंकु का वक्र पृष्ठीय क्षेत्रफल =\pi r l

शंकु का कुल पृष्ठीय क्षेत्रफल =\pi r l+\pi r^{2}, अर्थात् \pi r(l+r)

गोले का पृष्ठीय क्षेत्रफल =4 \pi r^{2}

अर्धगोले का वक्र पृष्ठीय क्षेत्रफल =2 \pi r^{2}

अर्धगोले का कुल पृष्ठीय क्षेत्रफल =3 \pi r^{2}

घनाभ का आयतन =l \times b \times h

घन का आयतन =a^{3}

बेलन का आयतन =\pi r^{2} h

शंकु का आयतन =\frac{1}{3} \pi r^{2} h

गोले का आयतन =\frac{4}{3} \pi r^{3}

अर्धगोले का आयतन =\frac{2}{3} \pi r^{3}

शंकु के छिन्नक का आयतन =\frac{1}{3} \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)
शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल =\pi l\left(r_{1}+r_{2}\right) जहाँ l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}
शंकु के छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल =\pi l\left(r_{1}+r_{2}\right)+\pi\left(r_{1}^{2}+r_{2}^{2}\right) 

Chapter – 14 सांख्यिकी (Statistics) formulas

👉प्रत्यक्ष विधि: \bar{x}=\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}

👉कल्पित माध्य विधि \bar{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}

👉पग-विचलन विधि: \bar{x}=a+\left(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\right) \times h

👉वर्गीकृत आँकड़ों का बहुलक सूत्र 

बहुलक =l+\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right) \times h

👉वर्गीकृत आँकड़ों का माध्यक सूत्र 

माध्यक =l+\left(\frac{\frac{n}{2}-\mathrm{cf}}{f}\right) \times h

Chapter – 15 प्रायिकता (probability)formulas

👉घटना E की सैद्धांतिक ( या परंपरागत) प्रायिकता P(E)

P(E)=\frac{A}{N}

A = प्रयोग के अनुकूल परिणामों की संख्या

N = प्रयोग के सभी संभावित परिणामों की संख्या 

👉एक निश्चित घटना की प्रायिकता P(E)=1 होती है।

👉एक असंभव घटना की प्रायिकता P(E)=0 होती है।

0 \leq P(E) \leq 1

👉किसी भी घटना E के लिए 

P(E)+P(\overline E)=1

जहाँ E घटना   \overline E (E नहीं ) को व्यक्त करता है E और   \overline E  पूरक घटनाएँ कहलाती हैं।

हम उम्मीद करते है आपको 👉 All Math’s formulas for class 10 in Hindi | सभी महत्वपूर्ण गणित के सूत्र कक्षा 10 👈 आर्टिकल बहुत अच्छा  लगा होगा और आपने इसे अभी तक अपने दोस्तों के साथ शेयर भी कर दिया होगा। 

यदि आप इसमें  किसी भी प्रकार का सूत्र या महत्वपूर्ण अवधारणा या कोई गलती का अभाव लगता हैं तो कमेंट करके आपका रिव्यु जरूर दीजिये 👍।