वृत्त किसे कहते हैं ? [circle formula in Hindi ] वृत्त से सम्बन्धित सूत्र

इस पोस्ट में, हमने  वृत्त किसे कहते हैं ? वृत्त से सम्बन्धित सूत्र से संबंधित सभी महत्वपूर्ण बातों को शामिल किया है। जैसे वृत्त सूत्र वृत्त का क्षेत्रफल और परिमाप/परिधि वृत्त का क्षेत्रफल सूत्र क्या है ? वृत्त की परिधि सूत्र क्या है ? वृत्त आधारित प्रश्न Circle based questions in Hindi  इन टॉपिक की सभी महत्वपूर्ण जानकारी दी गयी है। 

वृत्त किसे कहते हैं ?

एक वृत्त एक  वक्र के आकार का है, जहां वृत्त की सतह पर सभी बिंदु केंद्र बिंदु से समान दूरी पर हैं।

(x-h)² + (y-k)² = r²

जहाँ (x, y) समन्वय बिंदु हैं (h, k) एक वृत्त के केंद्र है और r एक वृत्त की त्रिज्या है।

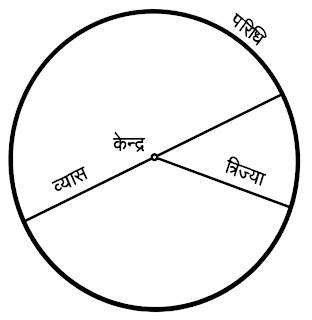
एक वृत्त के विभिन्न भाग त्रिज्या, व्यास, जीवा, स्पर्शरेखा, चाप, केंद्र  हैं।

वृत्त से सम्बन्धित शब्द  ( Terms related to Circle )   

• 👉त्रिज्या ( Radius ) : वृत्त के केन्द्र एवं परिधि पर के बिन्दु को जोड़ने वाली रेखा त्रिज्या कहलाती है ।  
• 👉जीवा ( Chord ) :  वृत्त के परिधि पर स्थित किसी दो बिन्दु को जोड़ने वाली रेखा जीवा कहलाता है ।  
• 👉व्यास ( Diameter ) वृत्त के केन्द्र गुजरने वाली जीवा व्यास कहलाता है । व्यास सबसे बड़ी जीवा होती है । 
• 👉चाप ( Arc of a circle ) : वृत्त का एक खंड चाप कहलाता है ।

वृत्त से सम्बन्धित सूत्र

यदि “r” वृत्त की त्रिज्या है, तो क्षेत्र और वृत्त की परिधि के सूत्र निम्न हैं:

वृत्त का क्षेत्रफल और परिमाप/परिधि

वृत्त का क्षेत्रफल = \pi r^{2}

वृत्त का परिमाप = 2\pi r

अर्द्धवृत्त का क्षेत्रफल =1/2 \pi r^2

अर्द्धवृत्त का परिमाप = (\pi + 2) r

चतुर्थास का क्षेत्रफल = 1/4 \pi r^2

चतुर्थास का परिमाप = (\frac{\pi}{2}+2)r

त्रिज्यखंड का क्षेत्रफल = \frac{\theta}{360^\circ}\times\pi r^2

चाप की लम्बाई = \frac{\theta}{360^\circ}2\times\pi r

वृत्त पर आधारित प्रश्न

Q.1 क्षेत्र और एक वृत्त की परिधि ज्ञात करें जिसका त्रिज्या 10 सेमी है। (Π = 3.14 का मान लें)

दिया गया: त्रिज्या = 10 सेमी।

क्षेत्र = π r²

= 3.14 × 102

A = 314 सेमी ²

परिधि, C = 2πr

C = 2 × 3.14 × 10

परिधि = 62.8 सेमी 

Q.2 एक वृत्त का क्षेत्रफल ज्ञात करें जिसकी परिधि 31.4 सेमी है।

SOL.  दिया हुआ: परिधि = 31.4 सेमी

एक सर्कल के क्षेत्र को खोजने के लिए, हमें त्रिज्या को खोजने की आवश्यकता है।

परिधि से, त्रिज्या की गणना की जा सकती है:

2 π r = 31.4

(2)(3.14)r = 31.4

r = 31.4 /(2)(3.14) = 10/2 = 5

इसलिए, वृत्त की त्रिज्या 5 सेमी है।

एक वृत्त का क्षेत्रफल πr² वर्ग इकाइयाँ है

अब, एक सर्कल सूत्र के क्षेत्र में त्रिज्या मान को प्रतिस्थापित करें, हमें मिलता है

A= 5 (5)²

A= 3.14 x 25

A = 78.5 सेमी²

इसलिए, सर्कल का क्षेत्रफल 78.5 सेमी²है।