Pythagoras theorem in Hindi

Pythagoras theorem in Hindi समकोण त्रिभुज की दो भुजाओं की लंबाई के वर्गों का योग कर्ण की लंबाई के वर्ग के बराबर है। 

Pythagoras Theorem (पाइथागोरस प्रमेय)

यह समकोण त्रिभुज के तीनो भुजाओ के बीच के संबंध की व्याख्या करता है। पाइथागोरस प्रमेय के अनुसार है कि “एक समकोण त्रिभुज में, कर्ण का वर्ग त्रिभुज के अन्य दो भुजाओ के वर्गों के योग के बराबर होता है। “

अन्य दो भुजा  यहाँ त्रिभुज के लंब  एवं  आधार हैं। अन्य दो पक्ष यहाँ त्रिभुज के लंबवत और आधार हैं। 90 ° कोण के सामने वाली भुजा को कर्ण कहते है 

Q.पाइथागोरस प्रमेय का कथन लिखिए व सिद्ध कीजिए

पाइथागोरस प्रमेय परिभाषा 

Q.पाइथागोरस प्रमेय का कथन बताइए 

पाइथागोरस प्रमेय में कहा गया है कि “एक समकोण त्रिभुज में, कर्ण का वर्ग अन्य दो भुजा के वर्गों के योग के बराबर है”। त्रिभुज के  भुजा को लंब, आधार और कर्ण का नाम दिया गया है। 

यहां, कर्ण सबसे लंबा  भुजा है, क्योंकि यह कोण 90 ° के विपरीत है। समकोण त्रिभुज (a, b और c) के भुजा का एक धनात्मक पूर्णांक मान होता है जब वर्ग को समीकरण में रखा जाता है,

पाइथागोरस त्रिक क्या है

जिसे पायथागॉरियन  त्रिक भी कहा जाता है।

पाइथागोरस प्रमेय का इतिहास 

प्रमेय का नाम एक ग्रीक गणितज्ञ के नाम पर रखा गया है जिसे पाइथागोरस कहा जाता है।

पाइथागोरस को किसका जनक कहा जाता है?

पाइथोगोरस एक गणितज्ञ का नाम था। , इनको को “संख्या के जनक” के रूप में जाना जाता है, पाइथागोरस प्रमेय भी इनके नाम से ही रखा गया है। 

पाइथागोरस प्रमेय सूत्र

यह  एक प्रमेय है जो एक समकोण त्रिभुज के तीनों भुजा के बीच संबंध दर्शाता है। इस प्रमेय को आमतौर पर निम्नलिखित तरीके से एक समीकरण के रूप में व्यक्त किया जाता है-

 कर्ण2 =  लंब2 + आधार2

AC^2 = AB^2 +BC^2

जहाँ AC एक समकोण त्रिभुज की कर्ण लंबाई है और AB और BC अन्य दो भुजाओं की लंबाई है।

पाइथागोरस प्रमेय Proof 

पहला तरीका 1st-method 

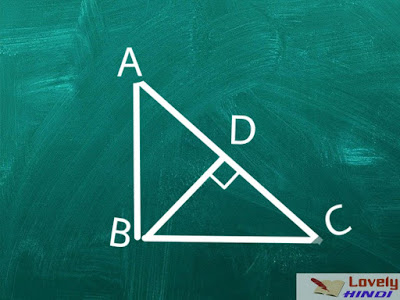
दिया गया: एक समकोण त्रिभुज ABC, B पर समकोण।

साबित करने के लिए

AC^2= AB^2 + BC^2

निर्माण: AC पर एक लम्ब BD खीचते है 

Proof-

हम जानते हैं, △ADB ~ △ABC

इसलिए, AD/AB = AB/AC (समान त्रिभुजों के संगत  भुजा)

या, AB2 = AD × AC ……………… (1)

इसके अलावा,△BDC ~△ABC

इसलिए, CD/BC = BC/AC (समान त्रिभुजों के संगत  भुजा)

या,  BC2= CD × AC ……………… (2)

समीकरणों को जोड़ना (1) और (2) हमें मिलता है,

AB2 + BC2 = AD × AC + CD × AC

AB2 + BC2 = AC (AD + CD)

चूंकि, AD + CD = AC

इसलिए, 

AC^2 = AB^2 + BC^2

Sinθ = लम्ब/कर्ण = AB/AC

Cosθ = आधार/कर्ण = BC/AC

sin²θ+Cos²θ = 1`

(AB/AC)²+(BC/AC)² = 1

(AB + BC)²/AC² = 1`

AB^2 + BC^2 = AC^2

पाइथागोरस प्रमेय के अनुप्रयोग

• यह जानने के लिए कि त्रिभुज एक समकोण त्रिभुज है या नहीं।

• समकोण त्रिभुज में, हम किसी भी पक्ष की लंबाई की गणना कर सकते हैं यदि अन्य दो पक्ष दिए गए हैं।

• एक वर्ग के विकर्ण को खोजने के लिए।

Pythagoras Theorem ke Questions

 

Sol.

 

 

 

 

एक वर्ग = 4 से.मी.

 

खोजने के लिए- विकर्ण एसी की लंबाई।

 

त्रिभुज abc पर विचार करें (या acd भी हो सकता है)

 

(ab)² +(bc)² = (ac)²

 

(4)² +(4)²= (ac)²

 

16 + 16 = (ac)²

 

32 = (ac)²

 

(ac)² = 32

 

ac = 4√2.

 

इस प्रकार, विकर्ण की लंबाई 4√2 cm सेमी है।