समतल में गति [ samtal me gati ] द्विविमीय गति
स्वागत है 🙏आपका , इस पोस्ट में समतल में गति [ samtal me gati ] द्विविमीय गति से संबंधित सभी महत्वपूर्ण जानकारी दी गई है।
समतल में गति [ samtal me gati ] द्विविमीय गति किसे कहते हैं ? एक उदाहरण दीजिए
किसी वस्तु की एक समतल में गति को द्विविमीय गति या समतल में गति कहा जाता है।
जैसे-तोप से छूटे गोले की गति
इस आर्टिकल में समतल में गति से सम्बंधित परिभाषाये , समतल में गति के कुछ महत्वपूर्ण बिंदु , समतल में गति के कुछ महत्वपूर्ण सूत्र को समावेश किया है, साथ में सभी महत्वपूर्ण सूत्र को अच्छे से लिखा गया है। फिर यदि कोई गलती है तो नीचे कमेंट में जरूर बताये ।
समतल में गति किसे कहते हैं ? द्विविमीय गति samtal me gati dvi-vimeey gati
समतल में गति ( Motion in a Plane )
जब कोई पिण्ड ऐसे त्वरण के अन्तर्गत गति करता है , जिसमें त्वरण की दिशा पिण्ड के प्रारम्भिक वेग की दिशा से भिन्न हो , तो पिण्ड के वेग का परिमाण तथा दिशा दोनों ही साथ – साथ बदलते रहते हैं , जिसके कारण पिण्ड एक समतल वक्र में गति करता है पिण्ड की इस गति को ‘ समतल में गति कहते हैं ।
जैसे — तोप से छूटे गोले की गति ।
द्विविमीय गति ( Motion in Two Dimensional )
वस्तु की गति द्विविमीय ( 2 D ) कहलाती है , यदि समय के सापेक्ष बदलते आकाश में वस्तु की गति दो निर्देशांकों से व्यक्त है ।
ऊर्ध्वाधर तल में क्षैतिज से किसी कोण पर फेंकी गयी वस्तु द्विविमीय गति का उदाहरण है । यह एक प्रक्षेप्य गति है ।
इसी प्रकार वृत्तीय गति भी द्विविमीय गति का उदाहरण है । किसी वस्तु की द्विविमीय गति , वेग अथवा त्वरण के दो परस्पर लम्बवत् घटकों से व्यक्त होती है ।
( i ) एकसमान त्वरण ( Uniform acceleration ) यदि एक कण की गति के दौरान त्वरण का परिमाण व दिशा नियत रहें , तो कण का त्वरण एकसमान त्वरण तथा गति एकसमान गति कहलाती है ।
( ii ) असमान ( परिवर्ती ) त्वरण ( Non – uniform acceleration ) यदि गति के दौरान कण के त्वरण का परिमाण अथवा दिशा दोनों परिवर्तित होते हैं , तो इसका त्वरण असमान ( परिवर्ती ) त्वरण कहलाता है ।
द्विविमीय गति में विस्थापन , वेग एवं त्वरण ( Displacement , Velocity and Acceleration in Two Dimensional Motion )
किसी वस्तु का विस्थापन उसके स्थिति सदिश के परिवर्तन से प्रदर्शित किया जाता है ।
\triangle r = r_f - r_i
किसी निश्चित समयान्तराल में वस्तु का औसत वेग उसके विस्थापन व समयान्तराल से प्रदर्शित किया जाता है ।
v =\frac{\triangle r}{\triangle t}👉यदि 𝚫t → 0 हो , तब औसत वेग , उस वस्तु का तात्क्षणिक वेग कहलाता है ।
\lim_{\triangle t \rightarrow 0}\frac{\triangle r}{\triangle t}= \frac{dr}{dt}तात्क्षणिक वेग की दिशा वस्तु के पथ पर गति की दिशा में स्पर्श रेखा की दिशा के अनुदिश होती है ।
वस्तु के वेग तथा समयान्तराल के अनुपात को औसत त्वरण कहते हैं ।
a =\frac{\triangle v}{\triangle t}👉यदि 𝚫t → 0 , तब औसत त्वरण उस वस्तु का तात्क्षणिक त्वरण कहलाता है ।
\lim_{\triangle t \rightarrow 0}\frac{\triangle v}{\triangle t}= \frac{dv}{dt}द्विविमीय गति ( Motion in Two Dimensional ) के उदाहरण
👉प्रक्षेप्य गति ( Projectile Motion )
यदि एक पत्थर को तिर्यक रूप से भूमि से फेंका जाता है , तो यह पृथ्वी की सतह के निकट गुरुत्व बल क्षेत्र ( वायु प्रतिरोध की अनुपस्थिति ) में गति करता है ।
इस प्रकार की गति प्रक्षेप्य गति कहलाती है तथा फेंकी गयी वस्तु को प्रक्षेप्य कहते हैं ।
👉वृत्तीय गति
वृत्तीय गति भी द्विविमीय गति का उदाहरण है । जब कोई कण वृत्त की परिधि के अनुदिश गति करता है, तो इस गति को वृत्तीय गति कहते हैं।
वृत्तीय गति, द्विविमीय गति अथवा एक तल में गति है।
किसी वस्तु की द्विविमीय गति , वेग अथवा त्वरण के दो परस्पर लम्बवत् घटकों से व्यक्त होती है ।
Read – वृत्तीय गति [Circular motion]
द्विविमीय आपेक्षिक गति (Relative Motion in Two Dimensions)
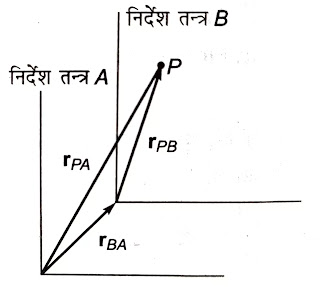
rPA= बिन्दु P का तन्त्र A के सापेक्ष स्थिति सदिश
rPB= बिन्दु P का तन्त B के सापेक्ष स्थिति सदिश
rBA= तन्र B का (मूल बिन्दु ) तन्र A के सापेक्ष स्थिति सदिश
तब
rPA =rBA+rPB
कण P के वेग
v_{PA} =v_{BA}+v_{PB}तथा
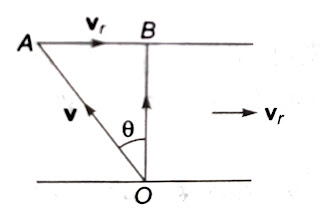
a_{PA} =a_{BA}+a_{PB}न्यूनतम समय में नदी को पार करने के लिए, नाव को सदैव धारा की दिशा के लम्बवत् चलाना चाहिए।
यदि नदी की चौड़ाई d तथा शांत पानी में नाव का वेग v है, तब
t=\frac{d}{v}O C=\sqrt{d^{2}+\left(v_{r} \frac{d}{v}\right)^{2}}न्यूनतम दूरी में नदी को पार करने के लिए, नाव को इस प्रकार गति करनी चाहिए ताकि इसके वेग का क्षौतिज घटक धारा के वेग को सन्तुलि करे।
पार करने का समय
\quad t=\frac{d}{\sqrt{v^{2}-v_{r}^{2}}}